Description

【题目背景】

尽管权王不让权王权王权，但是王权并不服气，于是他找到了权王要求商谈并希望能以理服人。然而双方的意见分歧实在太大，最终，他们还是选择了走向战场，用堂堂正正的战斗来说服对方……

【题目描述】

小W和小Q找到了一些特殊的石子，他们打算玩经典的取石子游戏。他们一共有$n$颗石子，这些石子样式各异，具有各不相同的美观程度 $b_i$ 和权值 $w_i$ 。凑巧的是，在 0 到 $n$ 这 $n+1$个数中，小W和小Q各自又对每个数字有不同的关注程度。我们认为，场上剩下的石子的数目所对应的小W和小Q的关注程度之和越高，比赛在那个时刻的紧张程度就越高。双方关注程度之和是一个定义在 $[0,n]$ 内整数集上的函数，记为 $c(x)$ 。简便起见，我们约定 $c(0)=0$ 。

由于石子十分漂亮，游戏过程中的气氛并不会一直那么紧张——这样美丽的石子总是让人赏心悦目的。然而，当场上石子的权值和与关注程度和的乘积大于场上石子的美观程度和与场上石子数目的乘积时，石子的外观就不再能够起到缓和气氛的作用了。由于小Q比小W来得Q，因此小Q只有在这个条件被满足的情况下才能得到一定的分数。

更加具体且形式化地，这场游戏的流程如下：

1.开始时把所有石子置入场内，双方初始分数均为0。

2.小W从场上石子中移除任意个（不可以移除0个）。移除后，小W获得 $\sum w_i$ 分。(求和等计算均针对仍留在场上的石子，下同）

3.小 Q从场上石子中移除任意个（可以移除 0个）。移除后，设场上石子数目为$m$，如果 $\sum m \times b_i < \sum c(m) \times w_i$成立，小 Q 获得$\sum m \times w_i$ 分。然后无论小 Q 是否获得了分数， 均将小Q移除的石子移回。

4.如果场上已经没有石子，游戏结束；否则回到第2步。

然而很不幸的是，小W和小Q早就凉了，没有人知道这场巅峰对决的结局。千百年后的今天，一位游吟诗人获知了他们所玩的游戏的规则，将它制作成了一款电子游戏供人娱乐。生活在今天的大W和大Q打算尝试一下这款游戏，大W扮演小W的角色，而大Q则扮演小Q。由于大W非常的 Q，因此大W 的目标是在最小化大 Q的分数的前提下最大化自己的分数，而大Q的目标是最大化自己的分数。

现在他们打开了游戏，石子的信息已经出现在了屏幕上。小W和小Q的亡魂想知道：如果大W和大Q均按照各自可能的最优策略行动，他们最终的得分分别会是多少？

Input Format

输入的第 1 行包含 2 个整数 $n$ 和 $case$ ，$n$ 表示石子的数量，$case$ 表示测试点编号。

接下来 1 行，包含 $n$ 个整数，其中第 $i$ 个表示 $b_i$ 。

接下来 1 行，包含 $n$ 个整数，其中第 $i$ 个表示 $w_i$ 。

接下来 1 行，包含 $n$ 个整数，其中第 $i$ 个表示 $c(i)$ 的值。约定$c(0)=0$。

Output Format

输出一行 2 个整数，依次表示双方均按最优策略行动时大 W 和大 Q 的最终得分

Sample

输入

4 3
1 2 3 4
4 3 2 1
1 2 3 4

输出

5 0

Hint

【样例 1 说明】 第 1 轮：大 W 移除 1 号和 2 号石子（按输入顺序编号），得到 $w_3+w_4=3$ 分；可以证明，该局面下大 Q 无论如何行动均无法得分。注意此时大 W 若移除 4 号石子将得到更高的总分， 但大 W 希望优先最小化大 Q 的分数（见题目描述），因此这里他不会选择移除 4 号石子。

第 2 轮：大 W 移除 4 号石子，得到 $w_3=2$ 分；大 Q 仍然无法得分。

第 3 轮：大 W 移除 3 号石子，游戏结束，大 W 最终得分为 5 分，大 Q 最终得分为 0 分。

【输入输出样例 2】

见下发文件中的 nim2.in 和 nim2.out。

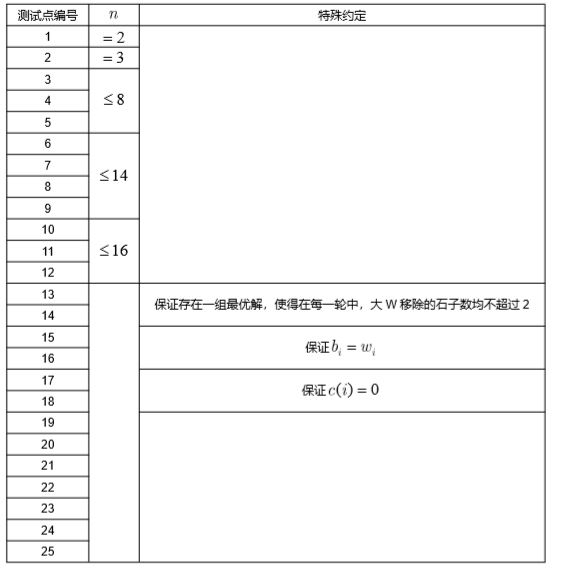
【数据范围与约定】

对于全部数据，有 $1 \le n \le 22$ ，$1 \le b_i,w_i \le 10000$ ， $ \left| （c_i） \right| \le 1000 $ 。

下表中留空的位置代表该测试点在这一项目上没有特殊约定。数据有一定梯度。