Description

【题目背景】 小 E 是一位实力强大的 OIer，经常在各类比赛中随手 AK 虐场。然而她最近秒题时遇到了 一道需要她思考 15 秒才能做出的题目，整整花了 15 倍于其他题目的时间。她认为这个问题 十分有意思，并且对其进行了一些拓展和修改以后抛给了你。你能接受小 E 的挑战吗？

【题目描述】

设 $p_i$ 表示非负整数 $p$ 的二进制表示中在项 $2^i$ 前的系数，对于非负整数 $p,q$ ，可以定义二元 运算$xnor$ （同或）为： $p$ $\text{xnor}$ $q=\sum_{i=0}^M ((p_i \land q_i) \lor (\lnot (p_i \lor q_i))) \times 2^i$（在这里我们认为布尔表达式的值 false 或 true 能够直接对应于整数0或1并参与算术运算， 反之亦然； 其中 $M$ 为常数，本题中 $M$ 的取值为31）。 给定一个长度为 $n$ 的非负整数序列 $a$，在序列的每个位置上有非负整数权值 $w_i$ ，现在希望实现对该序列的以下操作：

1. 给定区间 $[l,r]$ 和非负整数 $k$ ，查询 $(\sum_{i=l}^r a_i \times w'(i))$ $xnor$ $(\sum_{i=l}^r a_i)$ 。其中 $w'(i)=\begin{cases} w_i, if w_i \le k \\ 0 ,if w_i > k\end{cases}$

2. 给定正整数$p$ 和非负整数 $k$ ，将 $a_p$ 的值修改为 $k$。

3. 给定正整数$p$ 和非负整数 $k$ ，将 $w_p$ 的值修改为$k$ 。

Input Format

输入的第 1 行包含两个整数 $n, q$ ，$n$ 表示序列长度，$q$ 表示操作次数。

接下来 1 行，包含 $n$ 个整数，其中第 $i$ 个表示 $a_i$ 。

接下来 1 行，包含 $n$ 个整数，其中第 $i$ 个表示 $w_i$ 。

接下来 $q$ 行，每行包含 4 个或 3 个整数，其中第 1 个整数表示操作类型（见题目描述）。

对于第 1 种操作，接下来 3 个整数依次表示 $l,r,k$ ；对于第 2 或第 3 种操作，接下来 2 个整数依次表示 $p,k$ 。

Output Format

对于每个第 1 种操作输出一行一个整数，表示答案。

Sample

【输入输出样例 1】

输入

10 10
13 15 23 45 21 23 14 26 35 44
12 32 15 47 15 32 12 47 32 32
1 2 8 17
2 4 26
1 1 6 47
3 9 6
2 9 4
1 1 7 5
3 7 6
2 7 2
3 3 6
1 4 9 6

输出

4294966372
4294964016
4294967160
4294967229

Hint

【样例1说明】

对于第1次询问， $k = 17$ ，此时在 $[2,8]$ 区间内第3、第5和第7位置上的 $w_i \le 17$ 。因此答案为 $(a_3 \times w_3 + a_5 \times w_5 + a_7 \times w_7 )$ 。按照定义式计算即可得上式的值。 对于第3次询问，此时序列上的权值为$w = {12,32,15,47,15,32,12,47,6,32}$。 $k = 5$ ，但不存在 $w_i \le 5$ 的位置，因此答案为 $0$ $xnor$ $(\sum_{i=1}^7 a_i)$ 。

【输入输出样例2】

见下发文件中的challenge2.in和challenge2.out。

【数据范围与约定】

对于全部数据，有 $1 \le n,q \le 10^5$， $0 \le a_i,w_i,k \le 10^5$，$1 \le l,r,p \le n$ 。下表中留空的位置代表该测试点在这一项目上没有特殊约定。

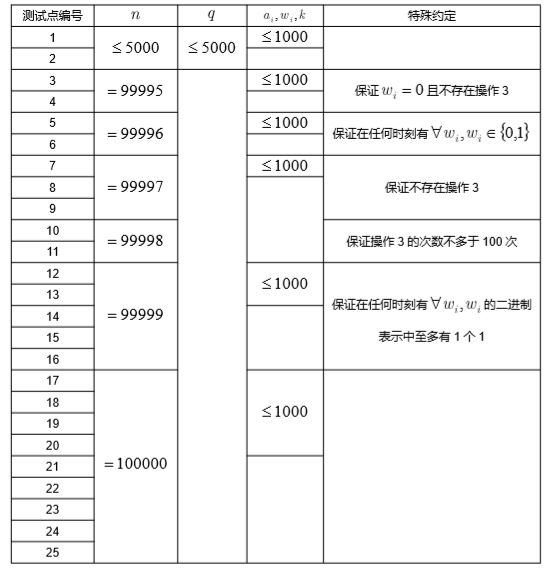
【提示】

$\land$ 表示逻辑与（即布尔代数中的与运算and），$\lnot$ 表示逻辑非（即布尔代数中的非运算not）。

由于本题时限较大，为节省评测时间，建议选手在程序中判断输入数据的规模并在程序会运行超时的数据点自行退出程序。